AcWing 789. 数的范围 二分 模板
标签:变化 scanf 方式 -- 的区别 区间更新 bsp cout name
https://www.acwing.com/problem/content/791/
#include<bits/stdc .h> using namespace std; const int N=100010; int n,m; int q[N]; int main() { scanf("%d%d",&n,&m); for(int i=0; i<n; i ) scanf("%d",&q[i]); while(m--) { int x; scanf("%d",&x); int l=0,r=n-1; while(l<r) { int mid=l r>>1; if(q[mid]>=x) r=mid; else l=mid 1; } if(q[l]!=x) cout<<"-1 -1"<<endl; else { cout<<l<<" "; int l=0,r=n-1; while(l<r) { int mid=l r 1>>1; if(q[mid]<=x) l=mid; else r=mid-1; //当更新方式为l=mid r=mid-1 } cout<<l<<endl; } } return 0; }
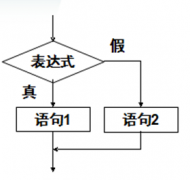
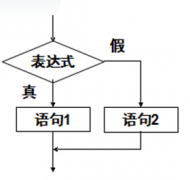
模板 这两个模板的区别在于去mid的时候是否 1 平时写的时候可以先不写 1, 然后当更新方式为l=mid, r=min-1时,再写上加1
解释 1:
举例子,因为时向下取整,当l=r-1,如果不补上 1,那么min=l r 1>>1=l 此时 如果说check时成功的 区间更新为l=mid=l 区间没有发生变化 ,那么下次循环也不会变,所以会形成死循环
当补上 1 mid会变成r 区间更新为l=mid=r 区间会从[l,r] 变成[r,r] 就不会发生死循环
bool check(int x) {/* ... */} // 检查x是否满足某种性质 // 区间[l, r]被划分成[l, mid]和[mid 1, r]时使用: int bsearch_1(int l, int r) { while (l < r) { int mid = l r >> 1; if (check(mid)) r = mid; // check()判断mid是否满足性质 else l = mid 1; } return l; } // 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用: int bsearch_2(int l, int r) { while (l < r) { int mid = l r 1 >> 1; if (check(mid)) l = mid; else r = mid - 1; } return l; } //整数二分
AcWing 789. 数的范围 二分 模板
标签:变化 scanf 方式 -- 的区别 区间更新 bsp cout name
温馨提示: 本文由杰米博客推荐,转载请保留链接: https://www.jmwww.net/file/14658.html