1. 概述

通过之前的教程，对WebGL中可编程渲染管线的流程有了一定的认识。但是只有前面的知识还不足以绘制真正的三维场景，可以发现之前我们绘制的点、三角形的坐标都是[-1,1]之间，Z值的坐标都是采用的默认0值，而一般的三维场景都是很复杂的三维坐标。为了在二维视图中绘制复杂的三维场景，需要进行相应的的图形变换；这一篇教程，就是详细讲解WebGL的图形变换的过程，这个过程同样也适合OpenGL/OpenGL ES，甚至其他3D图形接口。

可以用照相机拍摄照片来模拟这个图形变换的过程，如果要对某个物体拍摄照片，大致过程如下：

准备物体，把物体放置在某个合适的位置；这个过程就是模型变换（model transform）。

准备照相机，把照相机移动到准备拍摄的位置；这个过程就是视图变换（view transform）。

设置相机的焦距，或者调整缩放比例；这个过程就是投影变换（projection transform）。

对结果图形进行拉伸或者挤压，确定最终照片的大小；这个过程就是视口变换(viewport transform)。

而在WebGL/OpenGL中，具体的图形变换流程如下所示[3]：

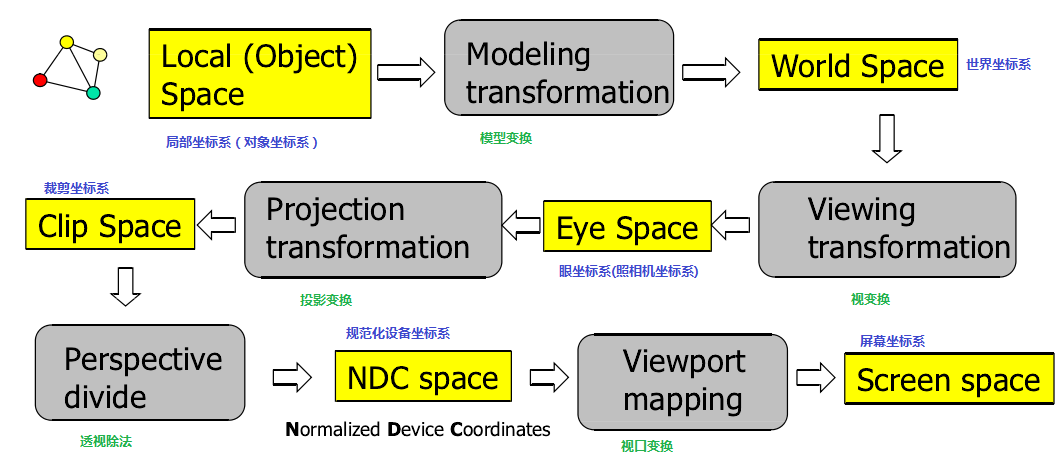
其中模型变换、视图变换、投影变换是我们自己在着色器里定义和实现的，而视口变换一般是WebGL/OpenGL自动完成的。这就好像我们拍照的时候，需要自己去调整位置，相机镜头焦距，而成像的过程就交给相机。所以模型变换、视图变换、投影变换这三者特别重要，另外附一张WebGL/OpenGL矩阵变换的流程图[4]：

从上两图中可以发现，场景中的物体总是从一个坐标系空间转换到另外一个坐标系空间。

局部坐标系（Local Space）指的是物体最初开始的坐标系；而世界坐标系（World Space）指的是物体与WebGL/OpenGL相机建立联系时的坐标系。这里的局部坐标系与世界坐标系跟通常意义的不同，只有与WebGL/OpenGL相机建立了联系，才是这里规定的世界坐标系。为了建立联系，经过的就是模型变换。

进入世界坐标系空间之后，物体与WebGL/OpenGL相机虽然建立了联系，但是并没有进一步确定观察物体的状态。这个时候就需要调整相机位置姿态，也就是视图变换，转换成视图坐标系（View Space），也可以简称为人眼坐标系（Eye Space），或者照相机坐标系（Camera Space）。

在人眼坐标系空间中，虽然物体就在眼前了，但是还需要进一步去确定可视空间。就像人眼是把水平视角大约200度左右的场景投影到视网膜中，人才能看清物体的那样，WebGL/OpenGL需要经过投影变换，才能正确的显示场景。这个过程通常还顺带进行了场景的裁剪，将可视空间范围外的东西去掉，所以投影变换后的坐标系就是裁剪坐标系（Clip Space）。

最后一步就是通过视口变换，从裁剪坐标系转换成屏幕坐标系，得到渲染结果。这一步由WebGL/OpenGL自动完成。

在参考文献[2]中描述的WebGL/OpenGL整个图形变换过程的坐标系和单位：

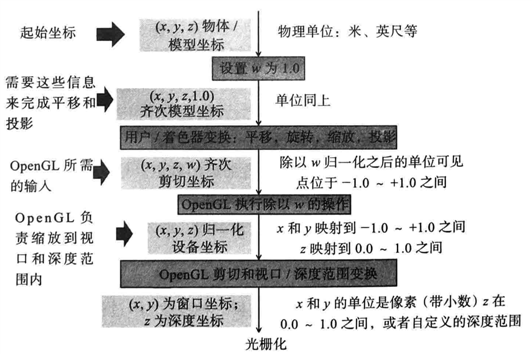
其流程与前文论述的基本一致，可以看到投影变换之后的过程不是那么简单，还需要将得到的齐次裁剪坐标做透视除法（除以w），做剪切和视口/深度范围变换，光栅化等。

其中，用户/着色器变换（也就是教程要具体详述的模型变换、视图变换和投影变换）包含坐标系和单位如下所示：

2. 详论

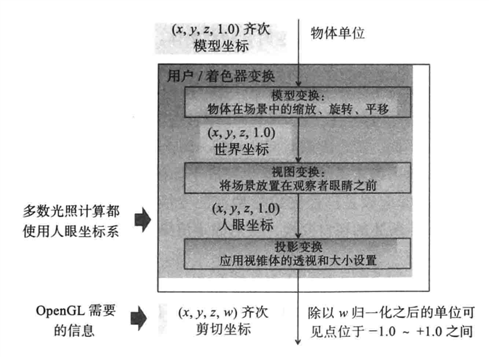
在一个三维软件中浏览一个三维物体时候，总是会提供给用户平移、缩放和旋转的交互操作，而这正是模型变换的内容。在图形学的范畴当中，平移变换、旋转变换属于刚体变换，缩放和旋转属于线性变换，刚体变换和线性变换又属于仿射变换，而仿射变换也可以看成投影变换的一种[5]。

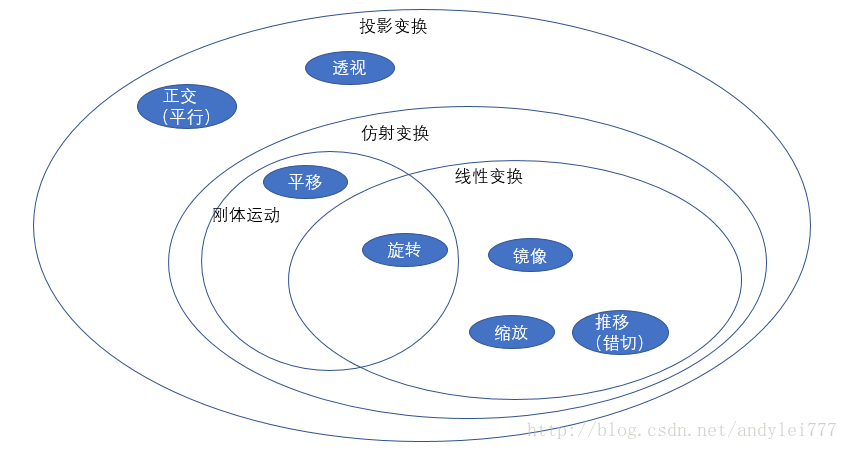
也就是说这些图形变换，本质上可以看成是同一种变换；在数学上，可以使用矩阵来描述这种变换。并且，为了兼容各种变换的特殊性，会在3维的基础上再加一维，使用4维的向量和矩阵。4维向量表述一个点（x,y,z,w）等价于三维向量（x/w,y/w,z/w），这就是前面提到的齐次坐标。

具体来说，对于空间某个点v0(x0,y0,z0,1),经过空间图像变换后得到新的点v1(x1,y1,z1,1),那么存在这样一个4行4列的矩阵M：