Netty作为一款高性能网络应用措施框架，实现了一套高性能内存打点机制

通过学习此中的实现道理、算法、并发设计，有利于我们写出更优雅、更高性能的代码；当使用Netty时碰到内存方面的问题时，也可以更高效定位排查出来

本文基于Netty4.1.43.Final介绍此中的内存打点机制

ByteBuf分类

Netty使用ByteBuf东西作为数据容器，进行I/O读写操纵，Netty的内存打点也是围绕着ByteBuf东西高效地分配和释放

当讨论ByteBuf东西打点，主要从以下方面进行分类：

Pooled 和 Unpooled

Unpooled，非池化内存每次分配时直接挪用系统 API 向操纵系统申请ByteBuf需要的同样巨细内存，用完后通过系统挪用进行释放
Pooled，池化内存分配时基于预分配的一整块大内存，取此中的部分封装成ByteBuf供给使用，用完后回收到内存池中

tips: Netty4默认使用Pooled的方法，可通过参数-Dio.netty.allocator.type=unpooled或pooled进行设置

Heap 和 Direct
Heap，指ByteBuf关联的内存JVM堆内分配，分配的内存受GC 打点
Direct，指ByteBuf关联的内存在JVM堆外分配，分配的内存不受GC打点，需要通过系统挪用实现申请和释放，底层基于Java NIO的DirectByteBuffer东西

note： 使用堆外内存的优势在于，Java进行I/O操纵时，需要传入数据地址缓冲区起始地点和长度，由于GC的存在，东西在堆中的位置往往会产生移动，导致东西地点变革，系统挪用堕落。为制止这种情况，当基于堆内存进行I/O系统挪用时，需要将内存拷贝到堆外，而直接基于堆外内存进行I/O操纵的话，可以节省该拷贝本钱

池化(Pooled)东西打点

非池化东西(Unpooled)，使用和释放东西仅需要挪用底层接口实现，池化东西实现则庞大得多，可以带着以下问题进行研究：

内存池打点算法是如何实现高效内存分配释放，减少内存碎片

高负载下内存池不停申请/释放，如何实现弹性伸缩

内存池作为全局数据，在多线程环境下如何减少锁竞争

1 算法设计 1.1 整体道理

Netty先向系统申请一整块持续内存，称为chunk，默认巨细chunkSize = 16Mb，通过PoolChunk东西包装。为了更细粒度的打点，Netty将chunk进一步拆分为page，默认每个chunk包罗2048个page(pageSize = 8Kb)

差别巨细池化内存东西的分配计谋差别，下面首先介绍申请内存巨细在(pageSize/2, chunkSize]区间范畴内的池化东西的分配道理，其他大东西和小东西的分配道理后面再介绍。在同一个chunk中，Netty将page凭据差别粒度进行多层分组打点：

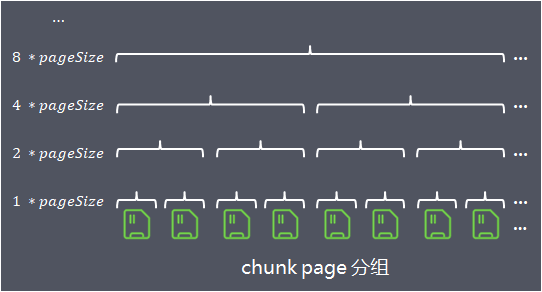
第1层，分组巨细size = 1*pageSize，一共有2048个组

第2层，分组巨细size = 2*pageSize，一共有1024个组

第3层，分组巨细size = 4*pageSize，一共有512个组
...

当请求分配内存时，将请求分配的内存数向上取值到最接近的分组巨细，在该分组巨细的相应层级中从左至右寻找空闲分组
例如请求分配内存东西为1.5 pageSize，向上取值到分组巨细2 pageSize，在该层分组中找到完全空闲的一组内存进行分配，如下图：

当分组巨细2 * pageSize的内存分配出去后，为了便利下次内存分配，分组被符号为全部已使用(图中红色符号)，向上更粗粒度的内存分组被符号为部分已使用(图中黄色符号)

1.2 算法布局

Netty基于平衡树实现上面提到的差别粒度的多层分组打点

当需要创建一个给定巨细的ByteBuf，算法需要在PoolChunk中巨细为chunkSize的内存中，找到第一个能够容纳申请分配内存的位置

为了便利快速查找chunk中能容纳请求内存的位置，算法构建一个基于byte数组(memoryMap)存储的完全平衡树，该平衡树的多个层级深度，就是前面介绍的凭据差别粒度对chunk进行多层分组：

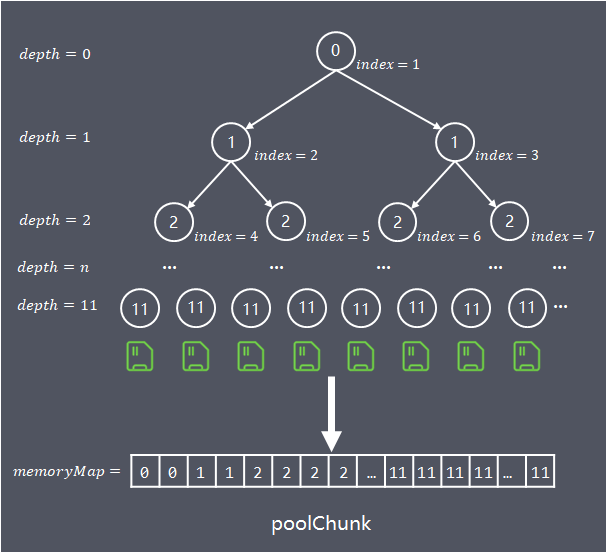
树的深度depth从0开始计算，各层节点数，每个节点对应的内存巨细如下：

depth = 0， 1 node，nodeSize = chunkSize depth = 1， 2 nodes，nodeSize = chunkSize/2 ... depth = d， 2^d nodes， nodeSize = chunkSize/(2^d) ... depth = maxOrder， 2^maxOrder nodes， nodeSize = chunkSize/2^{maxOrder} = pageSize

树的最大深度为maxOrder(最大阶，默认值11)，通过这棵树，算法在chunk中的查找就可以转换为：

当申请分配巨细为chunkSize/2^k的内存，在平衡树高度为k的层级中，从左到右搜索第一个空闲节点