标签：

On the "steerability" of generative adversarial networks Intro

本文提出对GAN的latent space进行操纵的一种要领，通过对latent space的编纂实现生成域外样本，操控生成样本的根基属性，如控制生成样本的位置、光照、二维旋转、三维旋转等等。

文章的主要孝敬为：

证明并实现了通过在latent space中的“walk”能够实现类似人类世界中相机的运动、颜色调动等操纵，这些操纵是通过自监督的方法学习到的。

不只能实现对输出域的线性调动，还能实现对输出域的非线性调动。

量化了数据集可学习到调动的最洪流平。

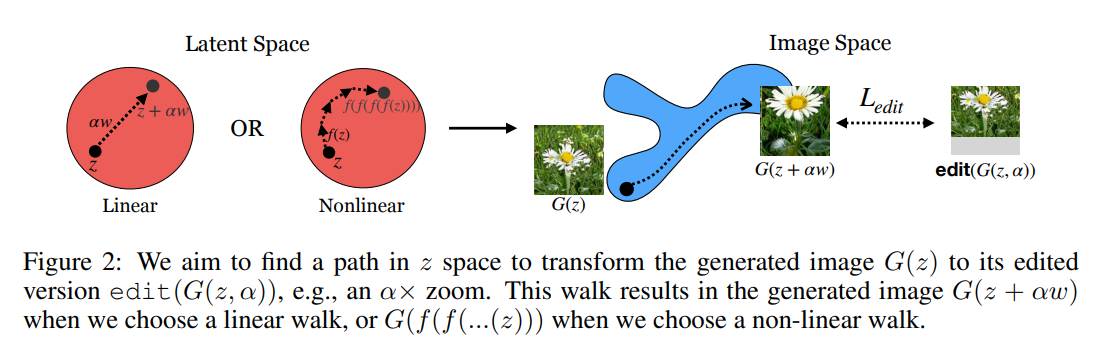
GAN颠末训练能够学习到一种映射，使得\(G(z) \rightarrow x\),也就是将latent space的采样功效映射为一图像漫衍下的样本。因此很自然就想到了，能否学习一种调动，使得对latent space的调动，也能映射到图像漫衍？作者称之为“walk”，即在latent space中执行某种调动，生成的图像也会做出相应的调动，以此来调治生成的图片，甚至可以生成域外样本。

Objective

\[ \omega^* = \mathop{argmin}_\omega \mathbb{E}_{z,\alpha}[\ell(G(z + \alpha \omega),edit(G(z),\alpha))] \]

上式edit是对生成的图像的调动操纵，\(\alpha\)是外部调治参数，\(\omega\)是可学习参数，看起来相当的简单。这里是认为G已经训练好了，即已经颠末反抗训练可以生成图片了。公式假设的是操纵是线性操纵，，实际上如果长短线性操纵就拟合一个对z的非线性函数，神经网络里往往用非线性激活拟合非线性，拟合的应该是一个step的变革。所以递归调动n次就是nstep的调动。
\[ \ell = \mathbb{E}_{z,n}[||f^n(z)-edit(G(z),n\epsilon)||] \]
此中n暗示第n个step，\(\epsilon\)暗示步长，\(f^n(z)\)是n次递归函数。

Quantifying Steerability

本文还提出调动前后量化比拟的指标，以量化调动的效果。

对付颜色调动，量化指标是随机抽取调动前后100 pixels像素值的变革，归一化到1.

对付zoom和shift的调动，量化指标是用一个方针检测网络输出物体中心位置，除以box的宽高归一化。

Reducing Transformation Limits

上面说了，是在G确定的情况下去学习latent space的调动，那么能否直接端到端训练呢？显然是可以的.
\[ G^*,\omega^* = \mathop{argmin}_{G,\omega}(\ell_{edit} + \ell_{GAN}) \]
直接端到端训练，GAN的loss凭据本来的，而编纂loss拿输入原图和编纂后的做loss即可。

尝试部分太长了，不感兴趣。

代码已开源：https://ali-design.github.io/gan_steerability/

[论文理解] On the "steerability" of generative adversarial networks