标签：sub   net   结果   ssi   ack   概率分布   sdn   strong   男人   

高斯混合模型

混合模型，顾名思义就是几个概率分布密度混合在一起，而高斯混合模型是最常见的混合模型；

GMM，全称 Gaussian Mixture Model，中文名高斯混合模型，也就是由多个高斯分布混合起来的模型；

概率密度函数为

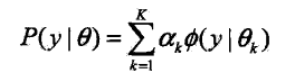
K 表示高斯分布的个数，α_k 表示每个高斯分布的系数，α_k>0，并且 Σα_k=1，

Ø(y|θ_k) 表示每个高斯分布，θ_k 表示每个高斯分布的参数，θ_k=(u_k，σ_k²)；

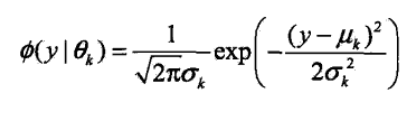
举个例子

男人和女人的身高都服从各自的高斯分布，把男人女人混在一起，那他们的身高就服从高斯混合分布；

高斯混合模型就是用混合在一起的身高数据，估计男人和女人各自的高斯分布

小结

GMM 实际上分为两步，第一步是选择一个高斯分布，如男人数据集，这里涉及取到某个分布的概率，α_k，

然后从该分布中取一个样本，等同于普通高斯分布

GMM 常用于聚类，也就是把每个概率密度分布聚为一类；如果概率密度分布为已知，那就变成参数估计问题

EM 解释 GMM

EM 的核心是 隐变量 和 似然函数

求导结果如下

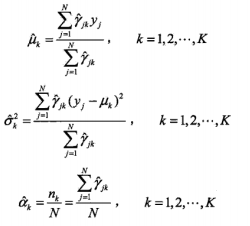
GMM 的 EM 算法

算法流程

参考资料：

https://blog.csdn.net/jinping_shi/article/details/59613054 

《统计学习方法》李航 

EM 算法(三)-GMM

标签：sub   net   结果   ssi   ack   概率分布   sdn   strong   男人