初始化的细节问题

我们看到的求最优解的背包问题题目中，事实上有两种不太相同的问法。
有的题目要求“恰好装满背包”时的最优解，有的题目则并没有要求必须把背
包装满。一种区别这两种问法的实现方法是在初始化的时候有所不同。
如果是第一种问法，要求恰好装满背包，那么在初始化时除了F[0]为0，其
它F[1..V ]均设为?∞，这样就可以保证最终得到的F[V ]是一种恰好装满背包的
最优解。
如果并没有要求必须把背包装满，而是只希望价格尽量大，初始化时应该
将F[0..V ]全部设为0。

这是为什么呢？可以这样理解：初始化的F数组事实上就是在没有任何物
品可以放入背包时的合法状态。如果要求背包恰好装满，那么此时只有容量
为0的背包可以在什么也不装且价值为0的情况下被“恰好装满”，其它容量的
背包均没有合法的解，属于未定义的状态，应该被赋值为-∞了。如果背包并非
必须被装满，那么任何容量的背包都有一个合法解“什么都不装”，这个解的
价值为0，所以初始时状态的值也就全部为0了。
这个小技巧完全可以推广到其它类型的背包问题，后面也就不再对进行状
态转移之前的初始化进行讲解。

01背包问题 题目描述

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi，，价值是 wi。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。
输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。
接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数，表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000

样例

输入样例：
4 5
1 2
2 4
3 4
4 5
输出样例：
8

朴素做法

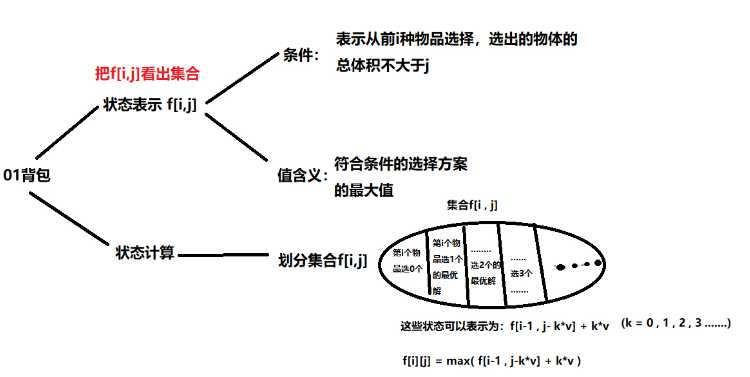
状态转移方程：
定义f[i][j]:前i个物品，背包容量j下的最优解
1）当前背包容量不够（j < w[i]），为前i-1个物品最优解：f[i][j] = f[i-1][j]
2）当前背包容量够，判断选与不选第i个物品
选：f[i][j] = f[i-1][j-w[i]] + v[i]
不选：f[i][j] = f[i-1][j]

时间复杂度&空间复杂度：均为O(V N) #include<iostream> #include<algorithm> using namespace std; const int N = 1010; int n,m; int f[N][N];// f[i][j]表示前i件物品恰放入一个容量为j的背包可以获得的最大价值 int w[N];//价值 int v[N];//重量 int main(){ cin>>n>>m; for(int i = 1;i <= n; i++){ cin>>v[i]>>w[i]; } for(int i = 1;i <= n;i++){ for(int j = 1; j <= m ;j++) if( j < v[i])//如果装不下，价值等于前i-1个物品 f[i][j] = f[i-1][j]; else //能装下，只考虑第i件物品的策略（放或不放） f[i][j] = max(f[i-1][j],f[i-1][j-v[i]]+w[i]); } for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) cout<<f[i][j]<<" "; cout<<endl; } return 0; } 优化空间复杂度为O（V），使用滚动数组

状态转移方程为：f[j] = max(f[j], f[j-w[i]] + v[i]

#include<iostream> #include<algorithm> using namespace std; const int N = 1010; int n,m; int f[N];// f[i][j]表示前i件物品恰放入一个容量为j的背包可以获得的最大价值 int w[N];//价值 int v[N];//重量 int main(){ cin>>n>>m; for(int i = 1;i <= n; i++){ cin>>v[i]>>w[i]; } for(int i = 1;i <= n;i++){ for(int j = m; j >= v[i];j--) f[j] = max(f[j],f[j-v[i]]+w[i]); } for(int i=1;i<=m;i++) cout<<f[i]<<" "; cout<<endl; return 0; } 完全背包

题目描述

有 N 种物品和一个容量是 V 的背包，每种物品都有无限件可用。
第 i 种物品的体积是 vi，价值是 wi。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。
输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。
接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 种物品的体积和价值。
输出格式
输出一个整数，表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000

样例

输入样例：
4 5
1 2
2 4
3 4
4 5
输出样例：
10

朴素做法

基本思路